资本资产定价模型(Capital Asset Pricing Model, CAPM)是现代金融市场理论的支柱,自其诞生以来,金融市场对资产风险分类的探索不断展开。CAPM的重要贡献是提出了Beta,即系统性风险,这种对于组合风险的细分研究使得对组合进行定量的风险管理和控制成为了可能。套利定价理论APT(Arbitrage Pricing Theory, APT)在CAPM的基础上,提出用更多因子来解释风险资产的收益。多因子模型(Multiple-Factor Model, MFM)基于APT理论的思想,发展出完整的风险模型。
多因子模型构建出风险资产预期收益与其持有者所承担风险的定量表达,不同因子代表不同风险类型的解释变量。多因子模型一般表达式:
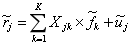
Xjk为股票j在因子k上的因子暴露;fk为因子k的因子收益;uj为股票j的残差收益率。
传统量化投资大多建立在这个模型之上,其本质是进行统计套利,通过对多种因子的挖掘,寻求相对稳定的超越市场基准的Alpha。BARRA模型是MSCI公司开发的一个经典的金融风险控制模型,其对宏观经济因子、基本面因子和统计因子三类因子进行了研究,发现基本面因子的模型效果要明显好于其他两类模型。需要指出的是,在BARRA框架之下,股票自身的属性如分红比例、财务数据、以及行情类指标K线等均被包括在“基本面因子”内。
本文将简单叙述多因子模型的构建流程,并对目前了解到的技术面因子进行整理。
参考华泰证券研究所,多因子模型基本构建流程如下:
一、准备工作
基础数据采集、数据标准化与有效因子的识别。对原始因子进行有效性检验,排除跟收益率相关性不高的因子。
二、收益模型
大类因子分析与因子共线性分析,即需对相关性很强的因子进行因子合成或择优处理,避免多重共线性对回归结果的影响;残差异方差分析,根据BARRA文档以及实践经验,采用个股流通市值的平方根作为权重进行加权最小二乘法回归,可在大部分截面数据上消除异方差的影响;确定模型并估计因子预期收益、计算股票预期收益。
三、风险模型
根据因子收益率的时间序列,计算因子协方差矩阵;计算个股残差风险并进行评估。
四、优化模型
确定组合收益风险目标;确定行业权重约束;确定因子暴露约束,避免在单个因子上暴露过大导致风险过高;确定个股权重上下限;根据限定条件,二次规划求解组合权重分配,构建投资组合并进行模拟业绩回溯。
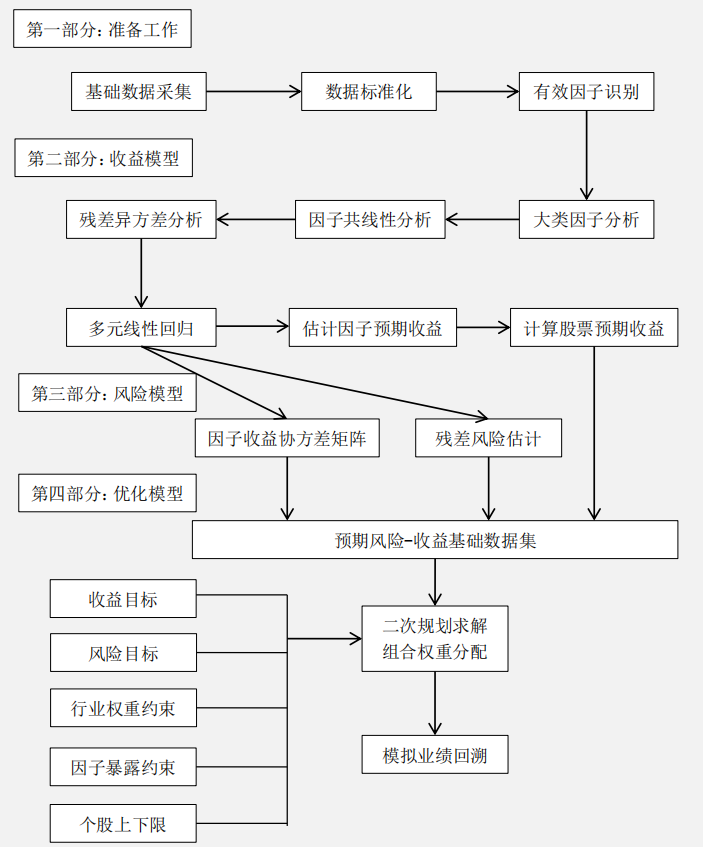
数据来源:华泰证券研究所
技术面因子于2015年正式成体系地呈现在公众面前。WorldQuant在2015年9月份公布的《101 Formulaic Alphas》研究报告中,以数据挖掘能力闻名业界的对冲基金 WorldQuant LLC 给出了它们正在使用,或曾经使用的101个阿尔法表达式。
国内券商研究所在此基础上,结合A股实际情况,对因子进行本土化处理并进行了检验。国泰君安2017年6月发布《基于短周期价量特征的多因子选股体系——数量化专题之九十三》,系统地整理了191个技术面因子,并使用这些因子构建组合进行模拟回测,在2012年1月至2017年4月之间,相较于中证500指数,实现年化超额收益50.2%,最大回撤5.9%,信息比率4.67。华泰证券于2016年下半年开始发布多因子系列报告,至今已陆续发布十余篇,内容涵盖估值类因子、成长类因子、动量类因子、换手率类因子、资金流向类因子、波动率类因子、财务质量类因子、一致预期类因子等。
从技术面因子分类来看,大可分为三类:1)动量因子;2)反转因子;3)混合因子。
动量因子即追随趋势,即“去头去尾只吃鱼身”,只要鱼身够大便可获得可观的收益。举例来说,下面这个因子最高价与最低价算数平均值减去成交量加权平均价,在成交量较少(较多)而价格快速拉升(下降)行情中,因子值为正(负)表示做多(做空)跟随倾向。
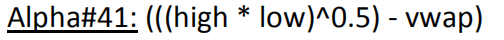
反转因子遵循均值回归的逻辑,与传统价值投资有着相同的理念,即资产价格在合理区间围绕其内价值波动,“低买高卖”赚取差价。举例来说,下面这个因子为开盘价与成交量相关性,与我们常讲的“底背离”相似,价格下降而成交量上升,是价格见底的一种信号。

第三类混合因子,即没有明显追踪趋势或均值回归的倾向。举例来说,下面这个因子为6日均价与数列[1,2,3,4,5,6]的回归相关系数,严格来讲应算作一种统计因子,对收益也具有一定程度的解释力。
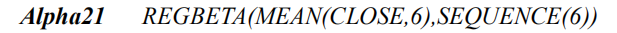
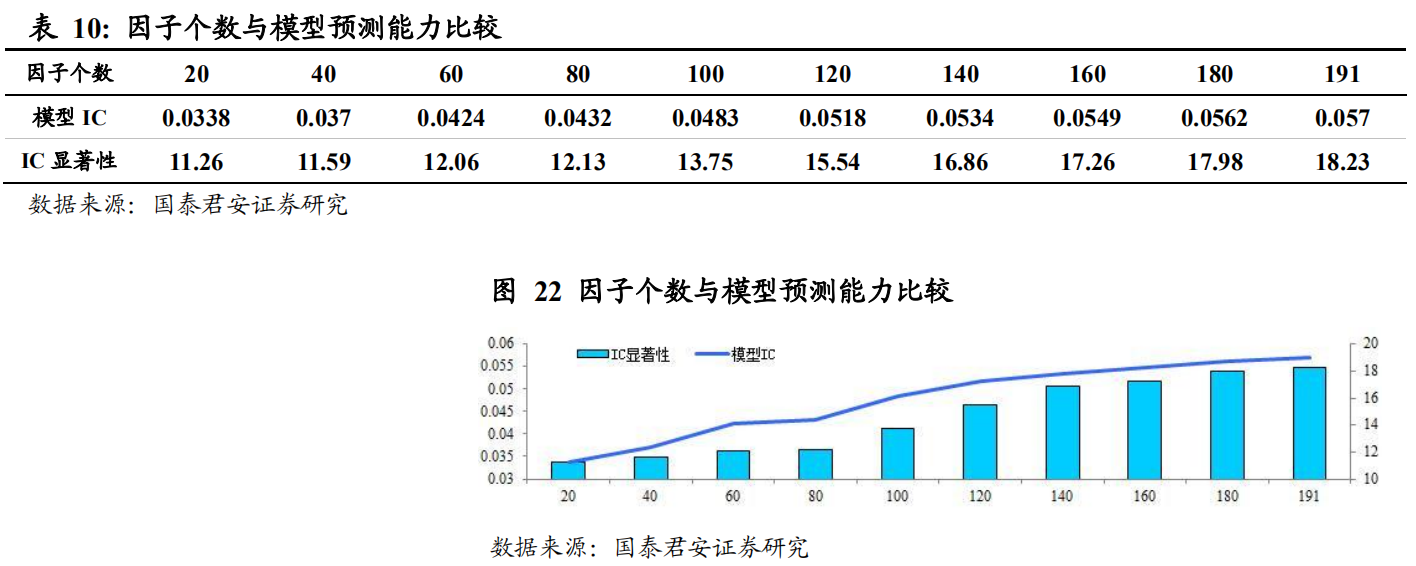
在底层因子构建完毕后,便可在此基础上进行因子组合,寻找更具解释力的复合因子,人工智能无论在因子构建还是因子组合方面均具备明显的优势。随着因子库不断扩充,模型对于市场收益的解释力也越强,这在国泰君安的研报中得到了一定验证。
参考文献:
Kakashadze, Z. (2016). 101 formulaic alphas. Social Science Electronic Publishing, 2016(84), 72–81.
国泰君安《基于短周期价量特征的多因子选股体系——数量化专题之九十三》,2017
华泰证券《华泰证券多因子系列》,2017,2018,2019
















